1.Định nghĩa:
Ma
trận là bảng chữ nhật chứa dữ liệu (số thực hay số phức) theo hàng
và cột, có dạng sau:
Hay
Ma trận thường được kí hiệu bởi các chữ cái A, B, C, . . .
Ma
trận với m hàng và n cột được gọi là ma trận cỡ m x n.
Hai
ma trận trên còn được kí hiệu:
A
= (aij)mxn
B
= [aij]mxn
1) Nếu m = n thì A gọi là ma
trận vuông cấp n.
Ví dụ: Ma trận vuông cấp
3.
2) Ma trận với chỉ một hàng gọi là ma trận hàng.
Ví dụ:
B = (2 4 5)
3) Ma trận với chỉ một cột gọi là ma trận cột.
Ví dụ:
4) aij gọi là phần tử trên hàng i và cột j của ma trận.
Ví dụ:
Thì a23 = 5 và a31= 3.
5)
Ma trận chuyển vị, kí hiệu AT
của ma trận A, là ma trận nhận được
từ ma trận A bằng cách
chuyển hàng thành cột (hay cột thành hàng).
Đó
là, nếu A = (aij) là ma trận cỡ m x n, thì AT = (bij) là ma trận cỡ
n x m
với
bij = aji.
a. Ví dụ: Cho
Thì
b. Tính chất của phép chuyển vị:
Cho
A và B là những ma trận và k là một số. Thì:
a)
(A + B)T = AT + BT
b)
(AT)T = A
c)
(kA)T = kAT
d) (AB)T = BTAT. Đó là, chuyển vị của tích là tích của chuyển vị, theo thứ tự ngược lại.
6) Ma trận với mọi phần tử bằng 0
gọi là ma trận không, kí hiệu 0.
Ví dụ: Ma trận không 2 x 3
7) Hai ma trận A và B gọi là bằng nhau, viết A = B, nếu chúng có cùng cỡ và nếu các phần tử tương ứng bằng nhau.
2.
Các phép toán ma trận
1) Cộng ma trận
a. Định nghĩa:
a. Định nghĩa:
Cho hai ma trận A = (aij)m×n,
B = (bij)m×n cùng cỡ m × n.
Tổng của A và B, kí hiệu A +
B, được định nghĩa là:
A + B = (cij)m×n,
với cij = aij + bij.
Chú ý: Tổng của những
ma trận khác cỡ không được định nghĩa.
b. Ví dụ: Cho hai ma trận cùng
cỡ 2 x 2
Tổng của hai ma trận A và B là:
c. Định nghĩa:
a) -A = (-)A.
b) A – B = A + (-B).
Ma trận –A gọi là
ma trận âm của A.
d.
Tính chất của cộng ma trận:
Cho
bất kỳ ma trận A, B, C cùng cỡ, ta có:
a)
(A + B) + C = A + (B + C)
b)
A + 0 = 0 + A = A
c)
A + (-A) = (-A) + A = 0
d)
A + B = B + A
e)
Theo a và d, thì bất cứ tổng của những ma trận:
A1 + A2 + … An
không
cần dấu ngoặc và không theo thứ tự.
2)
Nhân một số với ma trận
a.
Định nghĩa:
Cho số k và ma trận A = (aij)m×n.
Tích
của k và A, kí hiệu k.A hay kA, được định
nghĩa là:
kA = k(aij)mxn.
b. Ví dụ: Cho 3 và ma trận A
cỡ 2 x 2
Thì
c. Tính chất của nhân một số với ma trận:
Cho
bất kỳ hai số k, k’ và ma trận A, B, C cùng cỡ, ta có:
a)
k(A+B) = kA + kB
b)
(k + k’)A = kA + k’A
c)
(kk’)A = k(k’A)
d)
1A = A
3)
Nhân ma trận
a.
Định nghĩa:
Ví dụ:
A = (2, -3, 5)
Chú ý:
b.
Định nghĩa:
Cho
A = (aij)mxp và B = (bij)pxn. Tích AB
được
định nghĩa là:
Ví dụ: Cho
Thì
c. Tính chất của nhân ma trận:
a)
(AB)C = A(BC)
b)
(A+B)C = AC + BC
c)
C(A+B) = CA +CB
d)
Phép nhân ma trận không giao hoán:
Ví
dụ: Cho A và B cùng cỡ 2x2
Thì
II.
Ma trận vuông
1.
Định nghĩa:
Ma
trận vuông là ma trận với cùng số hàng và số cột.
Ma
trận vuông n x n gọi là ma trận vuông cấp n.
Không
phải mỗi hai ma trận đều có thể cộng hay nhân.
Nhưng
bất cứ ma trận vuông nào cũng có thể cộng, nhân, và hoán vị
với
kết quả là một ma trận vuông.
Ví dụ:
1) Cộng ma trận
Ví dụ:
1) Cộng ma trận
3) Nhân một số với ma trận
4) Nhân hai ma trận
5) Ma trận chuyển vị AT của A
Cho
Thì
2. Đường chéo
Cho ma trận vuông A = (aij). Đường chéo hay đường chéo chính của A
gồm có những số a11,
a22, …, ann
là
những phần tử từ góc trái trên đến góc phải dưới của A.
Ví dụ: Đuờng chéo của ma trận cấp 4
3.Trace
1)
Định nghĩa:
Trace
của A, viết tr(A), là tổng của những phần tử trên đường chéo.
Đó
là,
2) Ví dụ:
3)Tính chất:
Cho
A = (aij) và B = (bij) là những ma trận vuông và bất cứ số
k. Thì:
a.
tr(A + B) = tr(A) + tr(B)
b.
tr(kA) = k(tr(A))
d.
tr(AB) = tr(BA)
4.
Ma trận đơn vị
1)
Định nghĩa:
Ma
trận vuông đơn vị cấp n, kí hiệu In hay I, là ma trận với 1 trên đường
chéo
và
0 ở những nơi khác.
Cho
bất cứ ma trận vuông cấp n, thì ma trận đơn vị I giống như 1. Đó là,
AI
= IA = A
Tổng
quát hơn, nếu B là ma trận cỡ m x n , thì BIn = ImB = B.
Cho
bất cứ số k, ma trận kI chứa k trên đường chéo và 0 ở những nơi khác,
được gọi là ma trận số, hợp với số k.
được gọi là ma trận số, hợp với số k.
2)
Ví dụ:
a.
Ma trận đơn vị cấp 2, 3
Ta thường không viết 0 khi không có nhầm lẫn, như ma trận thứ hai ỏ trên.
b.
Ma trận số cấp 2, 3 với k = 3
3) Hàm Kronecker delta được định nghĩa là:
Như vậy, ma trận đơn vị được định nghĩa là
.
5. Lũy thừa của ma trận
1)
Định nghĩa:
Cho
bất cứ ma trận vuông A. Lũy thừa của A được định nghĩa như sau:
A0
= I, A1 = A, A2 = AA, A3 = A2A, …,
An+1 = AnA.
2)
Ví dụ:
6. Ma trận khả nghịch
1)
Định nghĩa:
Ma
trận vuông A được gọi là khả nghịch, nếu có một ma trận B sao cho
AB
= BA = I.
Như
thế, ma trận B là duy nhất. Nghịch đảo của A, kí hiệu A-1.
2)
Chú ý:
a.
B là nghịch đảo của A nếu và chỉ nếu A là nghịch đảo của B.
b.
AB = I nếu và chỉ nếu BA = I. Như vậy, ta chỉ cần chứng tỏ một tích AB
hay
BA để xác định hai ma trận đã cho là những nghịch đảo.
3)
Ví dụ: Cho
Thì
7.
Những ma trận vuông đặc biệt:
1)
Ma trận chéo là ma trận vuông với các phần tử không ở trên đường chéo bằng 0.
Đó là, aij = 0 với mọi i ≠ j.
Đó là, aij = 0 với mọi i ≠ j.
Ví
dụ:
Có
hai loại sau:
a.
Ma trận tam giác trên là ma trận vuông với các phần tử dưới đường chéo bằng 0.
Đó là, aij = 0 với mọi i > j.
Đó là, aij = 0 với mọi i > j.
Ví
dụ:
b. Ma trận tam giác dưới là ma trận vuông với các phần tử trên đường chéo bằng 0.
Đó là, aij = 0 với mọi i < j.
Ví
dụ:
3) Ma trận đối xứng là ma trận vuông với các phần tử đối xứng qua đường chéo bằng nhau.
Đó là, aij = aji hay AT = A.
Ví
dụ:
4) Ma trận phản đối xứng là ma trận vuông với các phần tử phản đối xứng qua đường chéo bằng nhau.
Đó là, aij = -aji hay AT = -A.
Chú
ý: Các phần tử trên đường chéo của ma trận phản đối xứng phải là 0,
vì aii = -aii nghĩa là aii = 0.
vì aii = -aii nghĩa là aii = 0.
Ví
dụ:
5) Ma trận sơ cấp
Cho
ma trận A với hàng R1, R2, …, Rm, ta có 3 phép
biến đổi hàng sơ cấp sau:
E1.
(Đổi hàng): Đổi hàng Ri và Rj, kí hiệu
Ta có ma trận sơ cấp hàng khi ta thực hiện một phép biến đổi sơ cấp với hàng của một ma trận đơn vị I.
Ví
dụ:


























































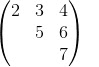

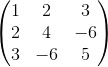







No comments:
Post a Comment